Operacje na zbiorach matematycznie i Linq
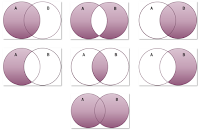Pisząc o Joinach chciałam dodać teorię zbiorów do całości obrazu.Jednak okazało się, że patrzyłam na to troszkę źle.
Relacje pokazywane na rysunkach zbiorów nie odnoszą się do samych JOIN'ów, a jedynie do elementu/zmiennej/zbioru zmiennych które łączą dwie kolekcje.
Użyjemy tego samego przykładu co poprzednio.
Teoria zbiorów ma zastasowanie tylko do TypeId ponieważ to był zawsze element łączący w Joinach.
Jeśli jednak porzucimy myślenie sqlami i składanie nowych obiektów w trakcie skomplikowanych joinów, pozostajemy z dodatkowymi funkcjami LINQ. Funkcjami które są odpowiednikiem teori zbiorów, nawet do poziomu nazw.
IEqualityComparer<T>
To najpiękniejszy interfejs do operacji na zbiorach.
Implementacja tego interfejsu określa nam matematyczny zbior elementów porównywanych.
Operując na obiekcie Girls można napisać kilka różnych implementacji, np takie:
Skoro mamy nasze Comaperar'y to teraz możemy zacząć myśleć o kolekcjach jak o zbiorach, zbiorach w których liczą się tylko pola porównywane. Porównujemy więc tylko te specyficzne wartości określone w IEqualityComaparer, należące do danego typu T, natomiast zwracamy listę, która zawiera pełne obiekty T spełniające warunek. Wszystko odbywa się na dwóch kolekcjach tego samego typu. Jeśli chcemy opererować na różnych typach, musimy wrócić do joinów.
To najpiękniejszy interfejs do operacji na zbiorach.
Implementacja tego interfejsu określa nam matematyczny zbior elementów porównywanych.
Operując na obiekcie Girls można napisać kilka różnych implementacji, np takie:
Skoro mamy nasze Comaperar'y to teraz możemy zacząć myśleć o kolekcjach jak o zbiorach, zbiorach w których liczą się tylko pola porównywane. Porównujemy więc tylko te specyficzne wartości określone w IEqualityComaparer, należące do danego typu T, natomiast zwracamy listę, która zawiera pełne obiekty T spełniające warunek. Wszystko odbywa się na dwóch kolekcjach tego samego typu. Jeśli chcemy opererować na różnych typach, musimy wrócić do joinów.
Iloczyn zbiorów
Matematycznie:
Iloczynem A ∩ B nazywa się zbiór tych elementów, które należą jednocześnie do obu zbiorów A oraz B. Iloczyn {1, 2, 3} oraz {2, 3, 4} to zbiór {2, 3}English: Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that are members of both A and B.
C#
Jedno proste słowo Intersect.public static System.Collections.Generic.IEnumerable<TSource> Intersect<TSource> (this System.Collections.Generic.IEnumerable<TSource> first, System.Collections.Generic.IEnumerable<TSource> second, System.Collections.Generic.IEqualityComparer<TSource> comparer);
Suma zbiorów
Matematycznie:
Sumą A ∪ B nazywa się zbiór tych elementów, które należą przynajmniej do jednego ze zbiorów A lub B. Suma {1, 2, 3} i {2, 3, 4} to zbiór {1, 2, 3, 4}.English: Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a member of A, or B, or both.
C#
Pierwszy rzut oka - możemy zrobić Concat. Ale wtedy dostajemy listę która zawiera wszystkie elementy z obu list, czyli także powtarzające się elementy, a tego nie chcemy.To czego szukamy to:
Union.
public static System.Collections.Generic.IEnumerable<TSource> Union<TSource> (this System.Collections.Generic.IEnumerable<TSource> first, System.Collections.Generic.IEnumerable<TSource> second);
Różnica zbiorów
Matematycznie:
Różnicą A \ B nazywa się zbiór tych elementów, które należą do zbioru A, ale nie należą do zbioru B. Różnica {1, 2, 3} \ {2, 3, 4} to {1} , natomiast różnica {2, 3, 4} \ {1, 2, 3} to {4}.English: Set difference of B and A, denoted B \ A, is the set of all members of B that are not members of A.
C#
Tutaj nie mamy już zgodności co do angielskiego określenia i nazwy funkcji, pozostaje nam logiczny odpowiedni.Jedno proste słowo Except.
public static System.Collections.Generic.IEnumerable<TSource> Except<TSource> (this System.Collections.Generic.IEnumerable<TSource> first, System.Collections.Generic.IEnumerable<TSource> second);
Ale możemy też bardziej skomplikowane operacje:
Różnica symetryczna
Matematycznie:
Różnicą symetryczną A △ B nazywa się zbiór tych elementów, które należą do jednego i tylko jednego ze zbiorów A oraz B, czyli elementy które są w jednym ze zbiorów, ale nie w obu zbiorach.English: Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of all objects that are a member of exactly one of A and B (elements which are in one of the sets, but not in both). For instance, for the sets {1, 2, 3} and {2, 3, 4} , the symmetric difference set is {1, 4} . It is the set difference of the union and the intersection, (A ∪ B) \ (A ∩ B) or (A \ B) ∪ (B \ A).
C#
W tym wypadku nie mamy jednej zgrabnej funkcji, musimy posłużyć się poprzednimi.var simetricDifference = listOne.Except(intersectedLists, nameComparer).Concat(listTwo.Except(intersectedLists, nameComparer));
Nie ma sensu tworzyć tutaj skomplikowanych funkcji dlatego taka metodka, która tylko demonstruje użycie z wypisaniem. Zaraz potem rzecz ważniejsza, czyli dane.
Bibliografia
Komentarze
Prześlij komentarz